Estimate Firestore collection count from a small sample of documents

This article shows a method of estimating the number of documents in a Firestore collection by reading only a small number of documents. It works if all documents in the collection use Firestore auto-IDs.

Important: this article may soon be obsolete as Firestore is adding built-in functionality to count the documents in a collection. I'm leaving it up for reference.

1. Introduction

Firestore is a NoSQL document database by Google. Firestore organizes data into collections, with each collection storing one or more documents. It excels at running fast queries on large datasets. However, it can't do some things you might be used to from SQL databases, like aggregation queries. You can't do a COUNT(*) on a firestore collection. If you want to know the number of documents in a collection, there are only two ways:

1. Read all documents and count them. This means downloading a large amount of data, and is also expensive since Firestore charges per document read (the charge is ~ $ 0.06 per 100k reads).
2. Write some code that is triggered when a document is added or removed, and updates a counter stored in a different collection, or somewhere else entirely. This is relatively cheap, but only works if you thought of it before you started your collection.

This article introduces a way of estimating the size of a collection by reading only a small number of documents.

2. Firestore document IDs

Every document in a firestore collection has a unique id, which can be almost any string. By default, firestore assigns auto-IDs, which are random strings of length 20 consisting of digits, capital letters and small letters. They look like this:

LH4KeuiVGnxdLS7KgYCW
McNZQ8dl14r8ppm8Up3N
s0EQSqAZUhMX0GKkccd1

Firestore also allows you to sort documents by their ID. This uses a simple lexicographic sort, where digits come before letters and capital letters before small letters.

3. Estimating collection size from document IDs

Let's consider the lexicographically smallest document IDs in your collection: If they cover a large portion of the available document ID space, this implies that your collection is small. If they cover a smaller portion, it implies that your collection is large.

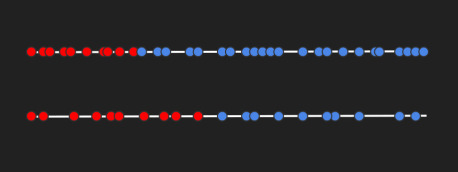
Illustration of the distribution of random document IDs. In a small collection, the 10 smallest IDs cover a large percentage of the available ID space. In a large collection, they cover a smaller percentage.

This allows us to estimate the size of a collection by looking at the first few documents ordered by ID.

3.1 A bit of math

We can think of the document IDs as numbers in base 62. The smallest ID would be 00000000000000000000 with a numerical value of 0, and the largest zzzzzzzzzzzzzzzzzzzz with a numerical value of $62^{20}-1$ , i.e. 704,­423,­425,­546,­998,­022,­968,­330,­264,­616,­370,­175.

Let's define: $M := 62^{20}$

This means that our document IDs are drawn from a uniform discrete distribution of integers in $[0, M[$

Let's call the $k$ smallest document IDs $x_1, ..., x_k$ , ordered from smallest to largest.

Then, we can estimate $n \\approx k \\frac{M}{x_k}$

3.2 A simple example

Let's say we have a collection with 25 million documents, and we read the first 1000. Let's also say that the 1000th document ID is 009NwyX2bgFfTrJbSyOF, which equals a numeric value of 27,­743,­012,­870,­072,­725,­675,­958,­771,­792,­799. Then our estimate would be:

$n_{est} = k \\frac{M}{x_k} = 1000 \\cdot \\frac{62^{20}}{27743012870072725675958771792799} \\approx 2.5391 E+7$

Which is very close to the real value of 25 million!

Because we read 1000 documents, we'd have to pay around $ 0.0006 for this estimate. Meanwhile, if we had read all 25 million documents, the charge would have been $ 15!

3.3 Improving our algorithm

Looking only at $x_k$ could lead to suboptimal results depending on the random distribution of document IDs. Instead, we can look at all of $x_1, ..., x_k$ , do the described calculation and average the results.

4. Code + a practical demonstration

Here's an example implementation in JavaScript:

const D0 = '0'.charCodeAt(0);
const D9 = '9'.charCodeAt(0);
const DA = 'A'.charCodeAt(0);
const DZ = 'Z'.charCodeAt(0);
const Da = 'a'.charCodeAt(0);
const Dz = 'z'.charCodeAt(0);

/** Convert a base62 digit to a number */
function digit(char) {
    const d = char.charCodeAt(0);
    if (D0 <= d && d <= D9) {
        return BigInt(d - D0);
    }
    if (DA <= d && d <= DZ) {
        return BigInt(d - DA + 10);
    }
    if (Da <= d && d <= Dz) {
        return BigInt(d - Da + 36);
    }
    throw new Error('invalid base62 digit: ' + char);
}

/** Convert a base62 string to a BigInt */
function id2Number(id) {
    let n = 0n;
    for (let i = 0; i < id.length; i++) {
        n += digit(id.charAt(id.length - i - 1)) * (62n ** BigInt(i));
    }
    return n;
}

const max = id2Number('zzzzzzzzzzzzzzzzzzzz');

/**
 * Estimate the collection size from a list
 * containing the smallest few document IDs
 */
function estimateN(ids) {
    let estSum = 0n;
    for (let i = 0; i < ids.length; i++) {
        const x = id2Number(ids[i]);
        const estimate = BigInt(i) * max / x;
        estSum += estimate;
    }
    return estSum / BigInt(ids.length);
}

    

This post also includes a practical demo that you can play around with: Just enter values for $k$ and $n$ below and click the big button to simulate the algorithm right in your browser!

This will generate $n$ random document IDs, sort them, get the first $k$ , and estimate $n$ using the code above. You can then see the error compared to the real value of $n$ below.

If you enter a large number, the browser tab might freeze or crash, especially on mobile... so be aware of that. Anything below a million should be fine. Btw, you can use scientific notation like 25e6!